Feature Engineering

Note

Before creating new feature research the domain and do some literature review

Handaling different data¶

Text Data¶

Text Processing¶

Remove Html characters, punctuation
Stop word removal
Lower case conversion
Stemming : Porter Stemmer, Snowball Stemmer
Lemmitizatiom : break a sentence into word Ref1, Ref2

Text to Vectors¶

Bag of Words (BOW)¶

Semantic meaning of word is lost
Binary/Boolean BOW
Count BOW
Uni-gram/ Bi-gram/N-gram

TF-IDF Term Frequency Inverse Documents Frequency¶

Semantic meaning of word is lost Ref1 Ref2

Word2Vec¶

Ways to train a Word2Vec Dictionary: CBOW & Skipgram
CBOW predicts focus word given context words using an autoencoder model
Skipgram predicts context word given focus word using an autoencoder model with multiple softmax (=number of context words) (Computationally more expensive to train, but can work with smaller data and infrequent words)
Algorithmic optimisations for Skipgram and CBOW
- Hieraarchial Softmax - No of softmax needed = \(log_2(Vocab\ Size)\)
- Negatice Sampling - Update only a sample (based on frequency) of words including the target word
In Word2Vec or Avg Word2Vec, Semantic information is learned by the vector
References : Word Embedding | Tensorflow Reference | TFIDF Weighted Word2Vec

Positional Embedding¶

Semantic and information about the Position in a sentence is captured
Keras Position Embedding
Transformers : Absolute Or Relative Positional Embedding

BERT & DistillBERT¶

Can be used as replacement for word2vec

Note

Transformers are more efficient in parallel processing than LSTMs Reference 1, Reference 2

Categorical Data¶

One hot encoding
Mean value replacement or response coding

Time Series & Wave Form Data¶

Moving Window¶

Within a Moving Window of width \(w\) calculate mean, std dev, median, quantiles, max, min, max - min, local minimas, local maximas, zero crossing

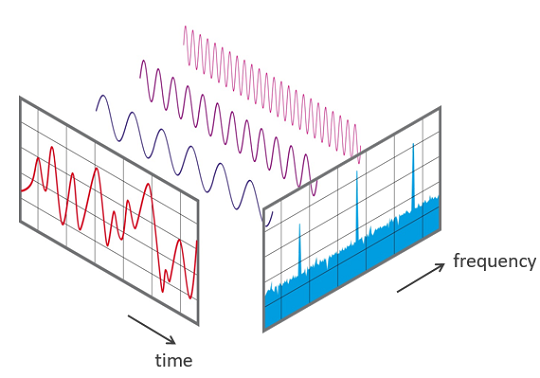
Fourier Transform¶

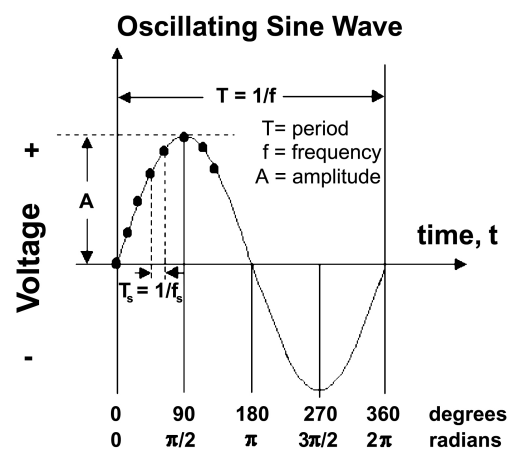
Any repeating pattern with Amplitude \(A\), Time Period \(T\), Frequency \(F\) and phase \(\phi\) can be broken down as sum of sine and cosines waves. Fourier Transform is used to convert a wave from Time domain to Frequency domain which is very insightful in repeating patterns

Discrete Fourier Transform (DFT)¶

The input is a sequence of numbers of the original variable (one value per time step)
The output is one value of amplitude (or signal strength) for each frequency. These are represented by the Fourier Coefficients.
This new series is computed using the Fourier formula:

\[X_k = \sum_{n=0}^{N-1} x_ne^{-2 \pi ikn/N}\]

Now we obtain the frequencies that are present in the variable. Each of the values in the outcome series is the strength of a specific frequency. If the amplitude of a frequency is high, then that seasonality is important in the orginal time series (or waves). There exists an Computational optimized form of DFT called Fast Fourier Transform. It is computed using the Cooley-Tukey FFT algorithm.

Graph Data¶

Node Level Features¶

Node InDegree and Node OutDegree¶

Eigenvector Centrality¶

Clustering Coefficient¶

DeepWalk¶

Graph coloring¶

HOPE¶

Page Rank ¶

Adar Index Kartz Centrality Shortest Path Connected-component HITS Score

Graph Level Features¶

Adjacency Matrix¶

Laplacian Matrix¶

Bag of Nodes¶

Weisfeiler-Lehman Kernel¶

Graphlet Kernels¶

Path-based Kernels¶

GraphHopper kernel, Neural Message Passing, Graph Convolutional Networks ¶

Neighbourhood Overlap Features¶

Local Overlap Measures¶

Global Overlap Measures¶

¶

Sequence Data¶

Image Data¶

Colour Image Histogram - Tutorial
Edge Histogams
Haar Features
SIFT Features : Very useful in Image Search with properties like scale invariance and rotation invariance

Graph Data¶