Skip to content

Useful Concepts in Machine Learning

Calibration of Models

When performing classification we often want not only to predict the class label, but also obtain a probability of the respective label. So after training a model, if this model is returning class labels and not returning the actual probabilities then we train a calibration moldel to calculate the probabilities. - Using \(D_{train}\) learn a function \(f(x)\) and using \(D_{cross \ validation}: \{x_i, y_i\}\) create a table of values \(x_i, \hat{y_i}, y_i\), sorted in increasing order of \(\hat{y_i}\) - Break the table into \(k\) chunks of size \(m\) and calculate \(mean \ y_i \ \forall \ j \ \epsilon \ k\) and call it \({y_{mean}^j}\) & \(mean \ \hat{y_i} \ \forall \ j \ \epsilon \ k\) and call it \({\hat{y}_{mean}^j}\) for each chunk - \(D_{calibration} : \{\ \hat{y}_{mean}^j, y_{mean}^j \}\) , Calibration Plot : \(y_{axis} = y_{mean}^j, \ x_{axis} = \ \hat{y}_{mean}^j\) - Now a Calibration function is trained to map \(\hat{y}_{mean}^j\) to \(y_{mean}^j\) (where \(y_{mean}^j\) is the probability if positive class) 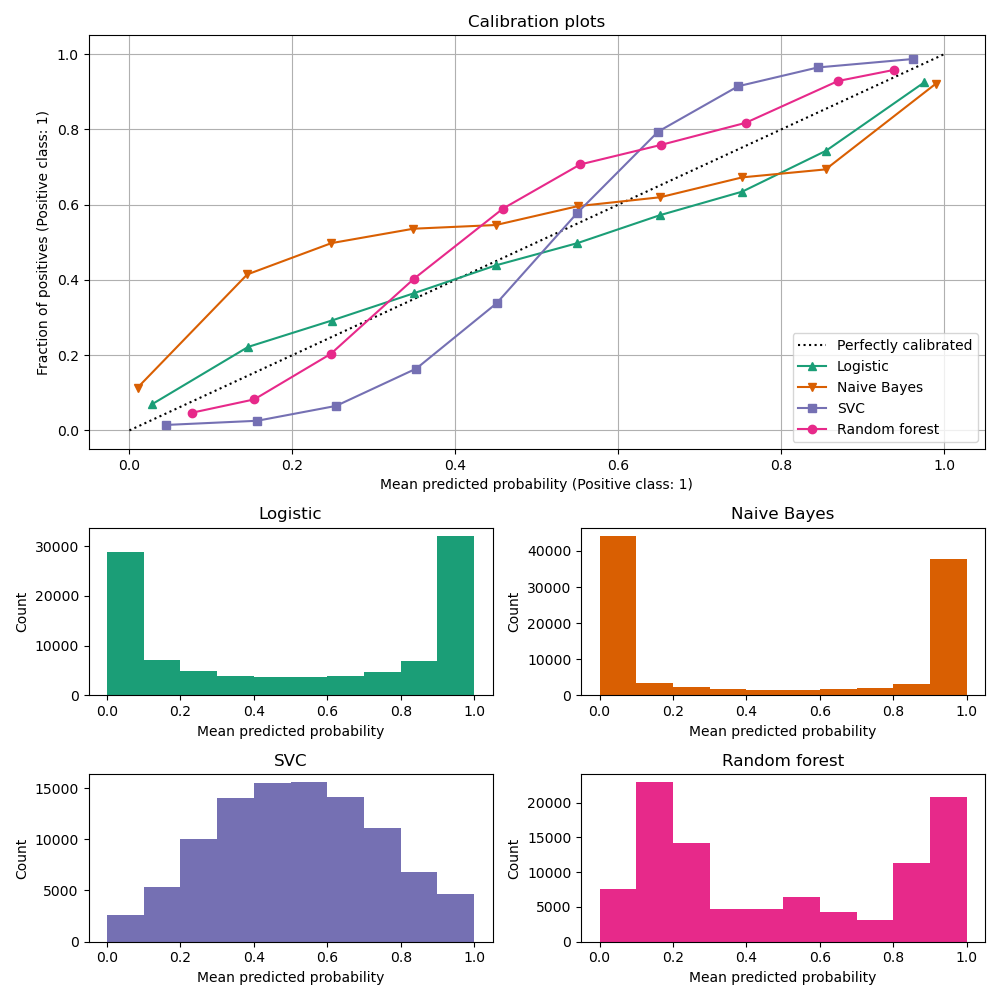calibration_plot - Platt Scaling Callibration : Works only if the calibration plot looks like sigmoid - Isotonic Regression Callibration : Learns Piece wise linear models, Works in almost all cases but needs more data than plat scaling - CalibratedClassifierCV  - Probability calibration of classifiers - Predicting Good Probabilities With Supervised Learning

Random Sampling Consensus (RANSAC)

  • Get a Random sample from \(D_{Train}\) call it \(D_0\) and build a Model \(M_0\) using \(D_0\)
  • Compute outliers dataset \(O_o\) using abolute error based on the \(M_0\) prediction
  • Now get the filtered data \(D_{train}^1 = D_{Train} - O_o\)
  • Repeat the above steps to get \(D_{train}^2, D_{train}^3 ...\)
  • When the \(M_i\) and \(M_{i+1}\) are very same then stop iterating and the \(M_{i+1}\) is a very robust model

Loss Minimisation Framework

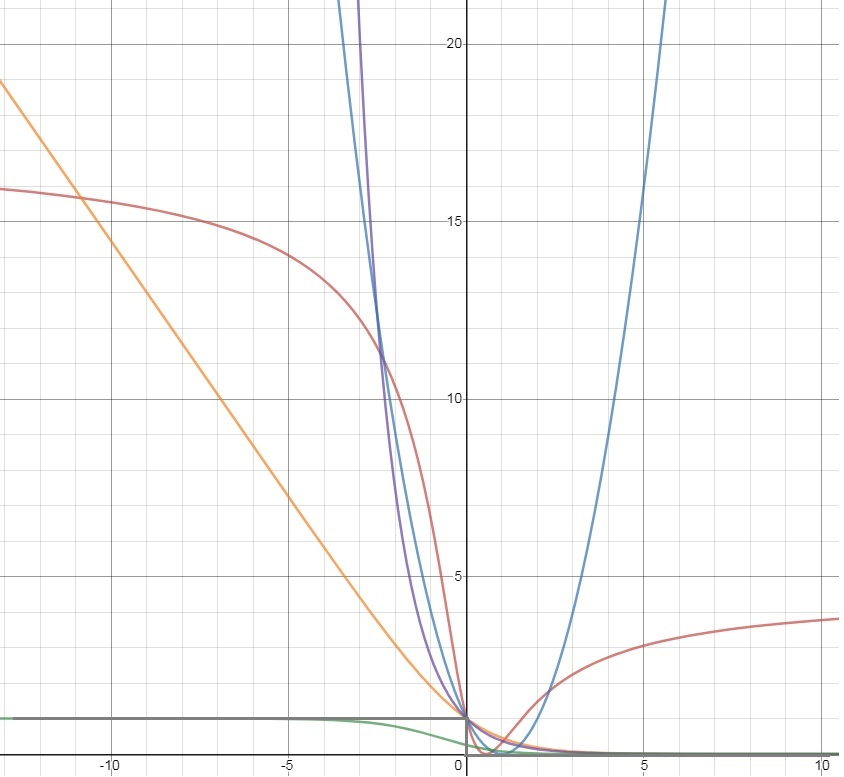
Loss functions for classification gray : Zero-one loss green: Savage loss orange: Logistic loss purple: Exponential loss brown: Tangent loss blue: Square loss

  • Logistic Regression : Logistic Loss (approximate of 0-1 loss) + Regulariser
  • Linear Regression : Linear Loss + Regulariser
  • SVM Regression : Hinge Loss + Regulariser

Hinge Loss : \(max(0, 1- y_i(w^Tx_i+b)) = \zeta_i\)

Reference

Overfitting, Underfitting, Variance, Bias and Generalisation

In general Overfitting results in High Variance Underfitting results in High Bias

If the data has high number of a constant value in prediction like : maximum 0s then Overfitting can result in High Bias

ToDo